INTRODUCING THE TOOL FOR REALIZING THE ETYMOLOGICAL ROOT OF THE MEANING OF “LOGARITHM,” RELATING IT TO DISCRETE GEOMETRY, VIA A CURVE OF A NAUTILUS MODEL [THE NATURAL SUBMARINE] .
“SPIRALOGORITHM” [name coined by Panagiotis Stefanides] Configuration of Photo 1, gives simple relationships between spirals and logarithms.
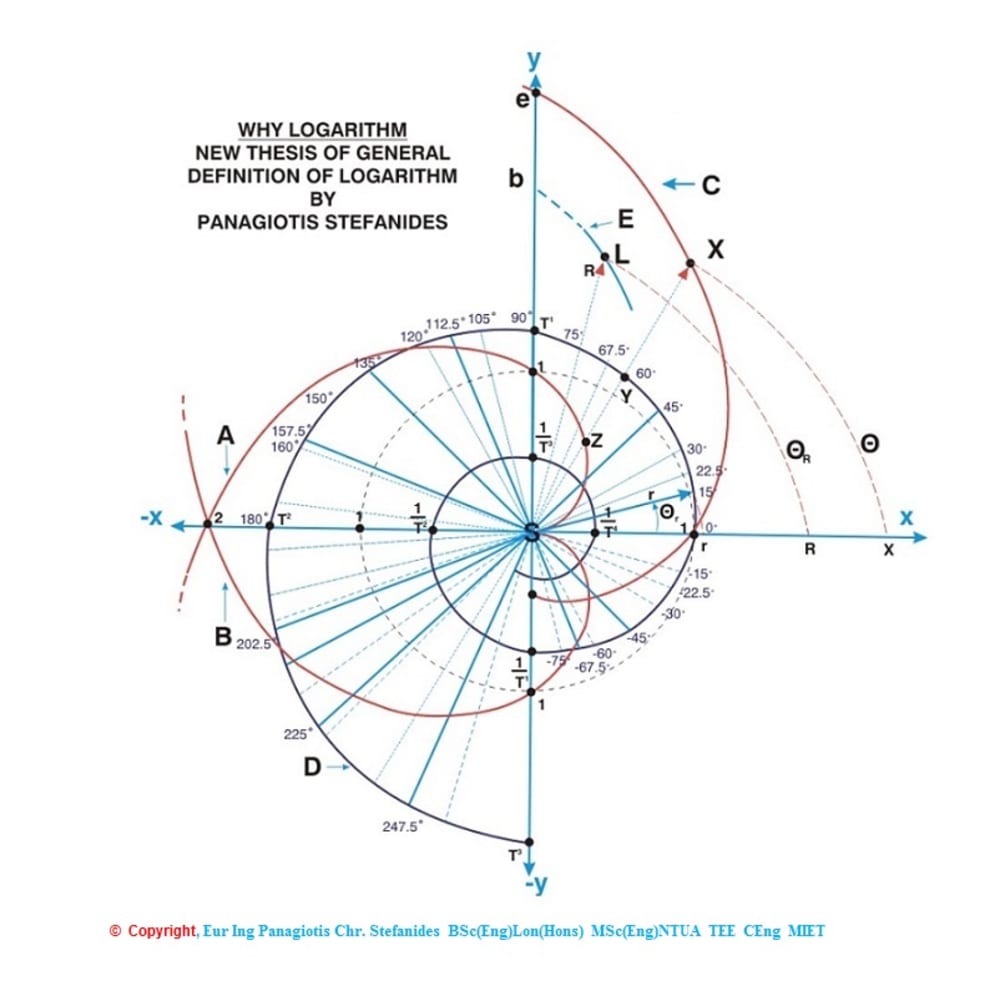
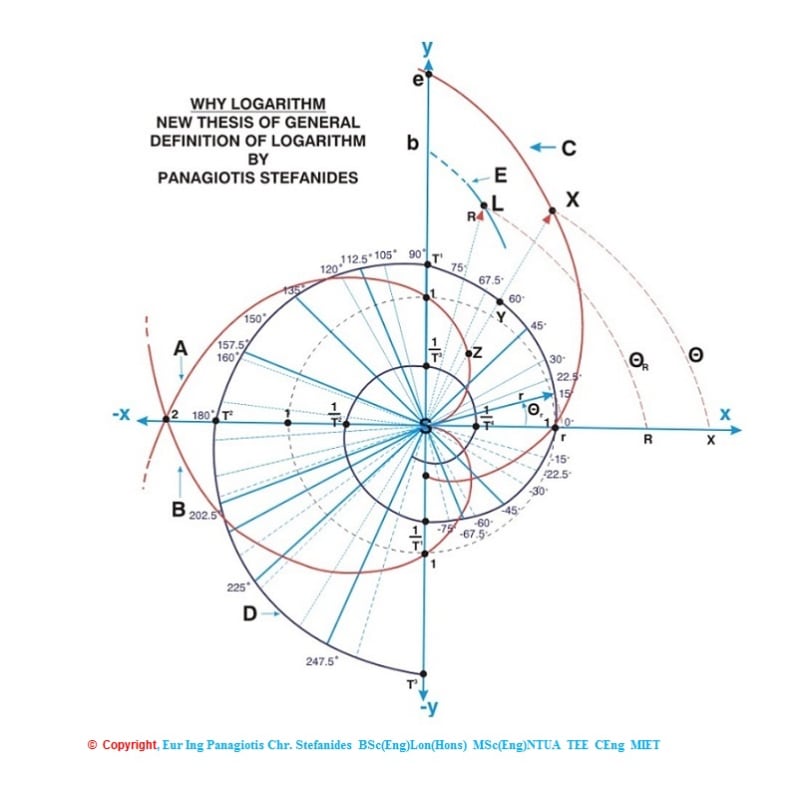
Introduced here is the STEPHANOID CURVE [author's proposal of nomination], the mirror images of two Archimedes curves of a special form, passing Zero [S] x-y point and on which lie vector length logarithms, of vector line lengths on the spiral[ one on top of the other]. Let X=e^[ Θ/90], be a point on the curve of this Spiral of Logarithmic base e ,on the plane of x-y coordinate system of Cartesian axes.
Phasor SX is at angle Θ from the x-axis taking anticlockwise direction as positive(Θ on x-axis is taken zero )and clockwise negative.
This Spiral crosses the [-y ] axis at point [ 1/e ], then the x axis at point 1 [moving anticlockwise], following crosses the y axis at point with value e, then the [-x] axis at e^2... etc...
This gives ln(X)=[ Θ/90], OR in RADIANS ln(X)= Θ/[Pi/2]. The 0 of the x y cross section is the assymptotic point of the Spiral. This theory is illustrated under: http://www.stefanides.gr/why_logarithm.htm TRANSFORMING [e^x] EXPANSION INVOLVING OTHER THAN [e ] BASES: e^x = 1+x+(x^2/2!)+(x^3/3!)+(x^4/4!)+(x^5/5!) may be transformed to other than e bases.
For instance, Lets for reasons that serve my web work(references below) , instead of x use Z where Z is a ral positive or negative number. So e^Z= 1+ Z+ [Z^2]/2!+…+..... Let X=e^Z , AND Log_e[X]=Z So X= 1 + Log_e[X] + {[Log_e[X] ]^2}/2!+.... Raise e^Z to the power of N (POSITIVE REAL NUMBER), we get e^[NZ]=1+NZ+{[NZ]^2}/2!+... Let e^N = T SO THAT Log_e[T]=N WHERE T is a POSITIVE REAL NUMBER [BASE OF ANOTHER THAN e LOGARITHM ], then, e^[NZ]= T^Z=1+Z[Log_e[T]] + [{Z[Log_e[T]]}^2]/2!+..... Let this T^Z = Y, or Log_T[Y]=Z AND ( from above ) Log_e[X]=Z = Log_T[Y] ,so X=e^{Log_T[Y]} =1+{Log_T[Y]} + = . AND Y=T^{ Log_e[X] }=1+ [{ Log_e[X]}*{Log_e[T]} ]+…+….or Y= 1+[{ Log_T[Y]}*{Log_e[T]} ] +…+…
According to this involved theory: Log_e[X] = Log_T[Y] ==Z= Θ( deg)/90=Θ(rad)/[Pi/2] For BASE T=1 then Y= T^Z=1 [ MODULUS (1) ,ARGUMENT (Θ) ] or 1^Z=1 [ MODULUS{sqrt[cos^2[theta] +sin^2[theta] }=1 ] , ARGUMENT (Θ) or 1^{ Θ/[Pi/2] }=1[ MODULUS ( 1) ,ARGUMENT (Θ) ] i.e. the ROOTS and POWERS of UNITY , And Log_1[1] = Z = Θ/90=Θ/[Pi/2]. This is the case of a CIRCLE, a DEGENERATED SPIRAL OF BASE 1 This CIRCLE passes points on x and y axes: x=1, y=1
Ref: http://www.stefanides.gr/why_logarithm.htm
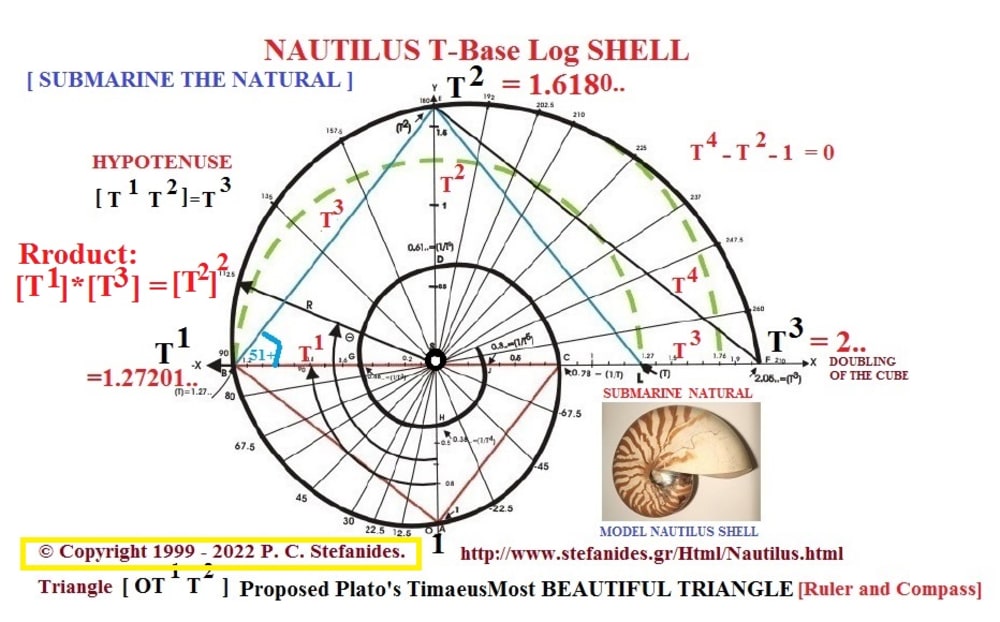
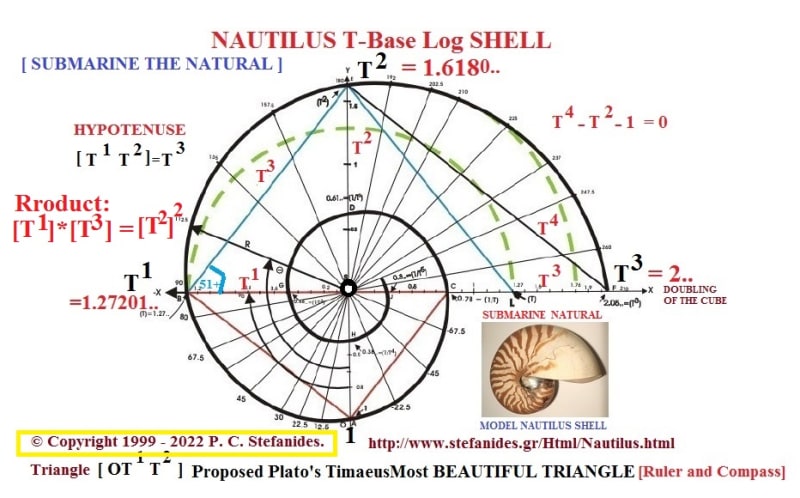
Photo 2 Show relevant Configurations of ORTHOGONAL LOGARITHMIC SPIRALS [SKELETONS of such ], and Photo 3 similarly the NAUTILUS Base T Logarithmic Spiral, where T the Square Root of the Golden number [Φ].
Ref: http://www.stefanides.gr
Video
Like this entry?
-
About the Entrant
- Name:Panagiotis Stefanides
- Type of entry:individual
- Software used for this entry:N/A
- Patent status:none