Below is the equation for the resistance of a fluid flow system:
∆P/Ǭ=(q-W)/VǬ-ρ δv/Ā-(μA_⟘ dv_⟘)/ĀǬ-(ρA_h gδh)/ĀǬ
Where Ǭ is the total volumetric flow in the system; ∆P is the pressure difference across the system; V is the volume of the system; Ā is the area perpendicular to the flow; A⟘ and dv_⟘are the area and velocity difference parallel to the flow; Ah and δh are the area and height of the system relative to gravity.
Each term on the right of the equal sign represents:
(q-W)/VǬ
The flow resistance due to energy (q) or work (W) done to or by the system.
-ρ δv/Ā
The flow resistance due to a velocity change δv
-(μA_⟘ dv_⟘)/ĀǬ
The flow resistance due to shear caused by a velocity gradient
-(ρA_h gδh)/ĀǬ
And last, the flow resistance due to a change in height and the effect of gravity. It was derived by applying the forces acting on a fluid element: pressure, inertial, gravity, and viscous or friction acting over a distance per unit time--which is power. Unlike the Navier-Stokes equation based on conservation of energy, a force acting over a distance is equal to a constant, the equation is linear allowing elements to be added or combined with ease.
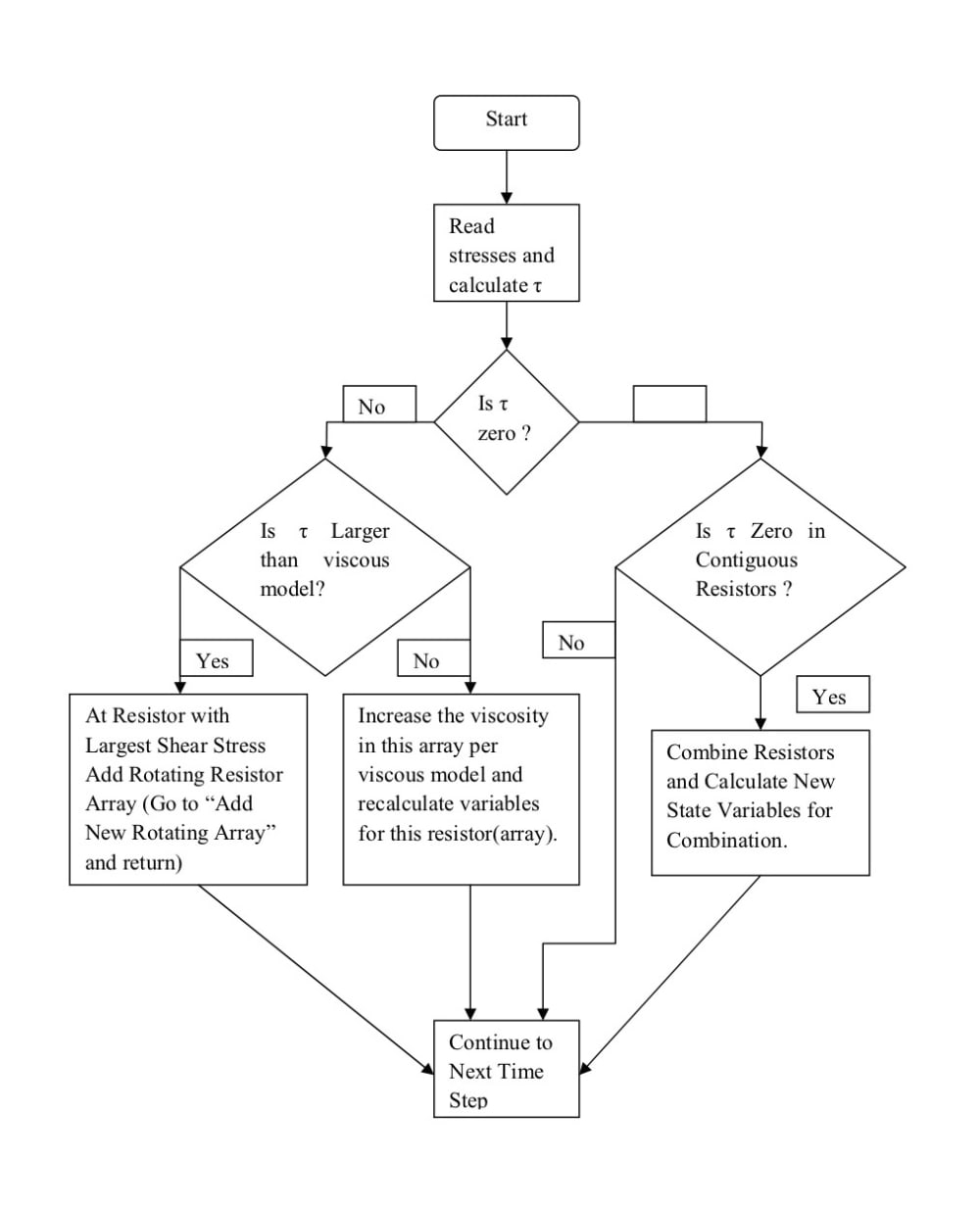
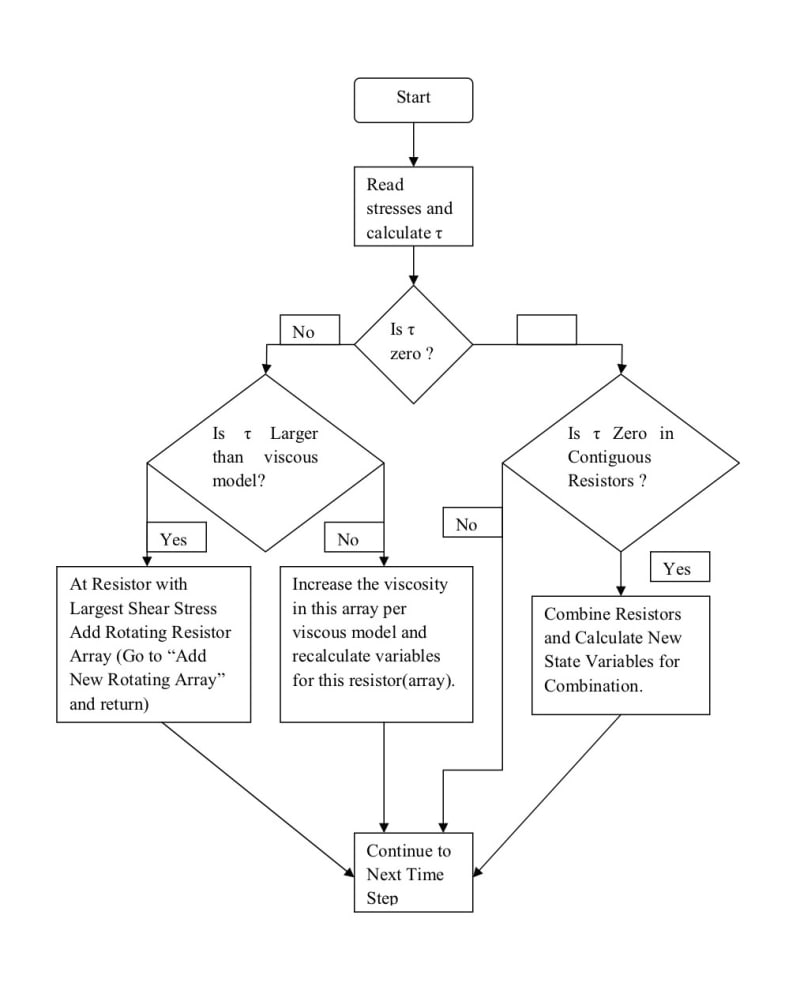
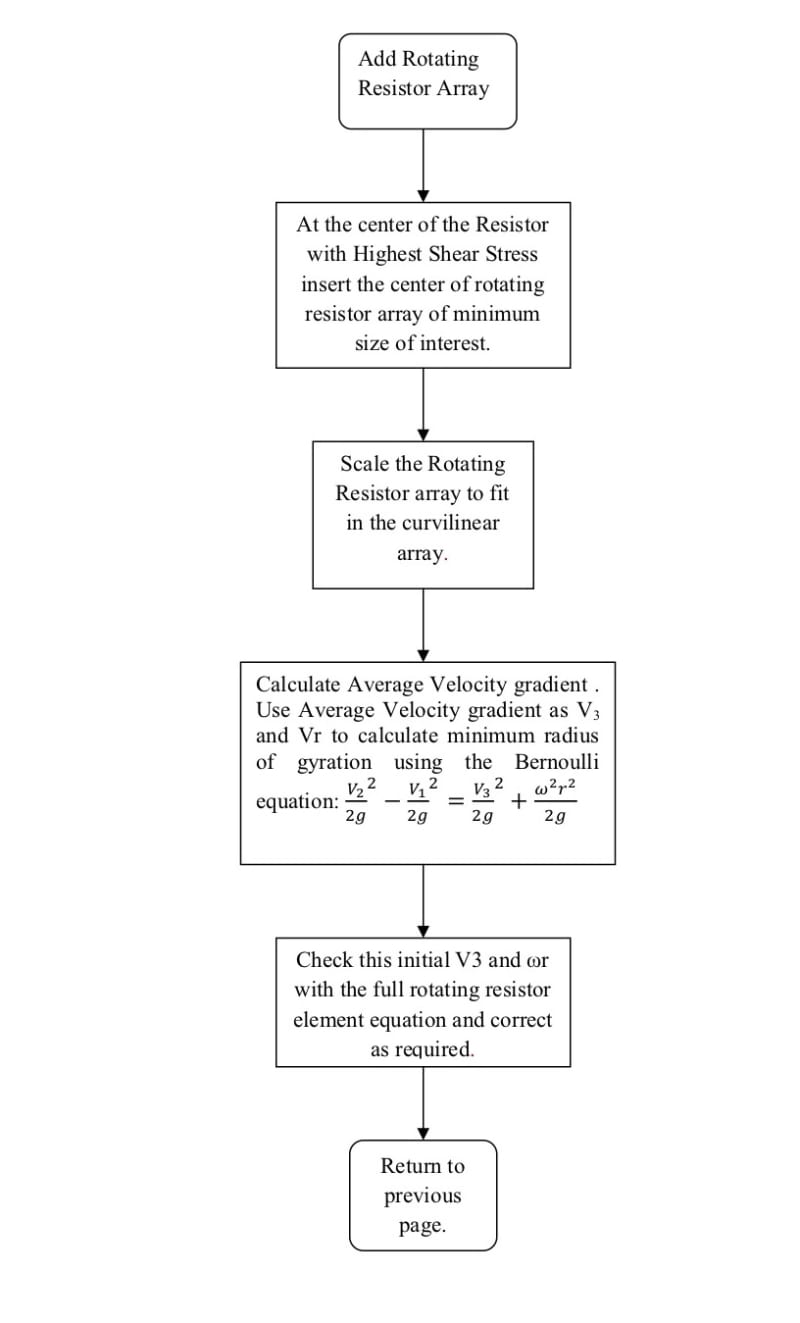
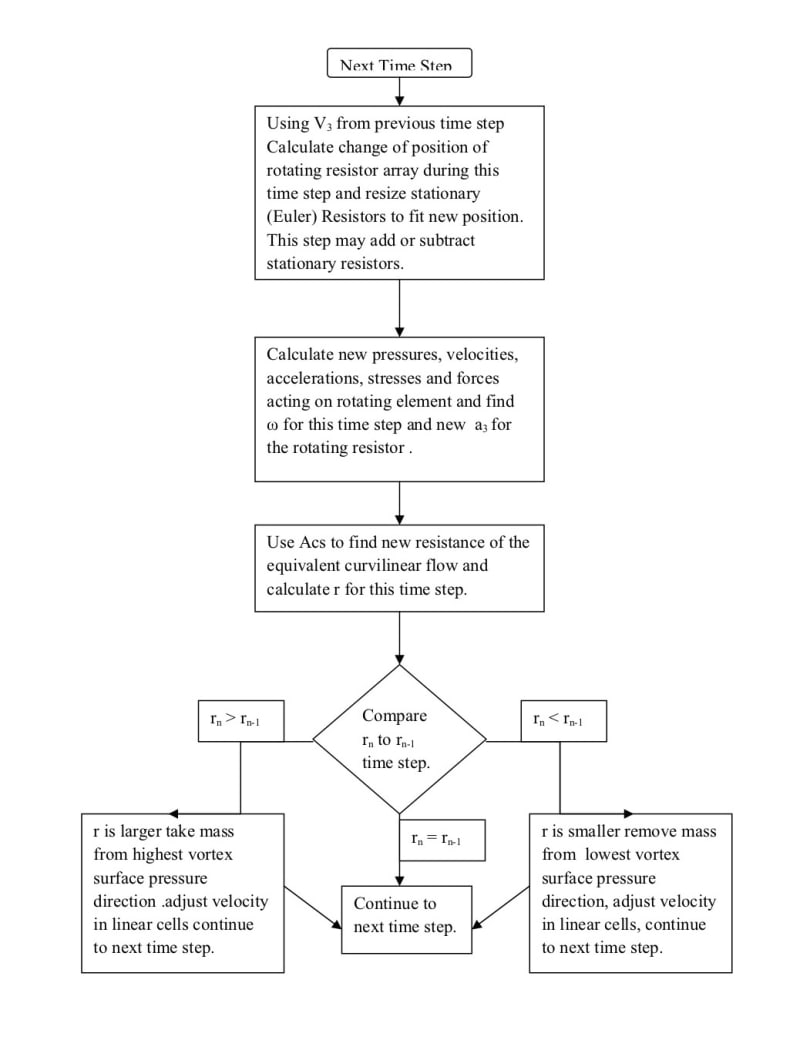
For example, if there is a velocity gradient due to a jet or boundary that caused a shear gradient tau with its attendant torque the resistance equation becomes:
∆P/Ǭ=(q-W)/VǬ-ρ δv/Ā-(μA_⟘ dv_⟘)/ĀǬ-(ρA_h gδh)/ĀǬ+Fr ω/Ǭ^2 -ρr^2 (ω^2-〖ω_0〗^2)/2Ǭ
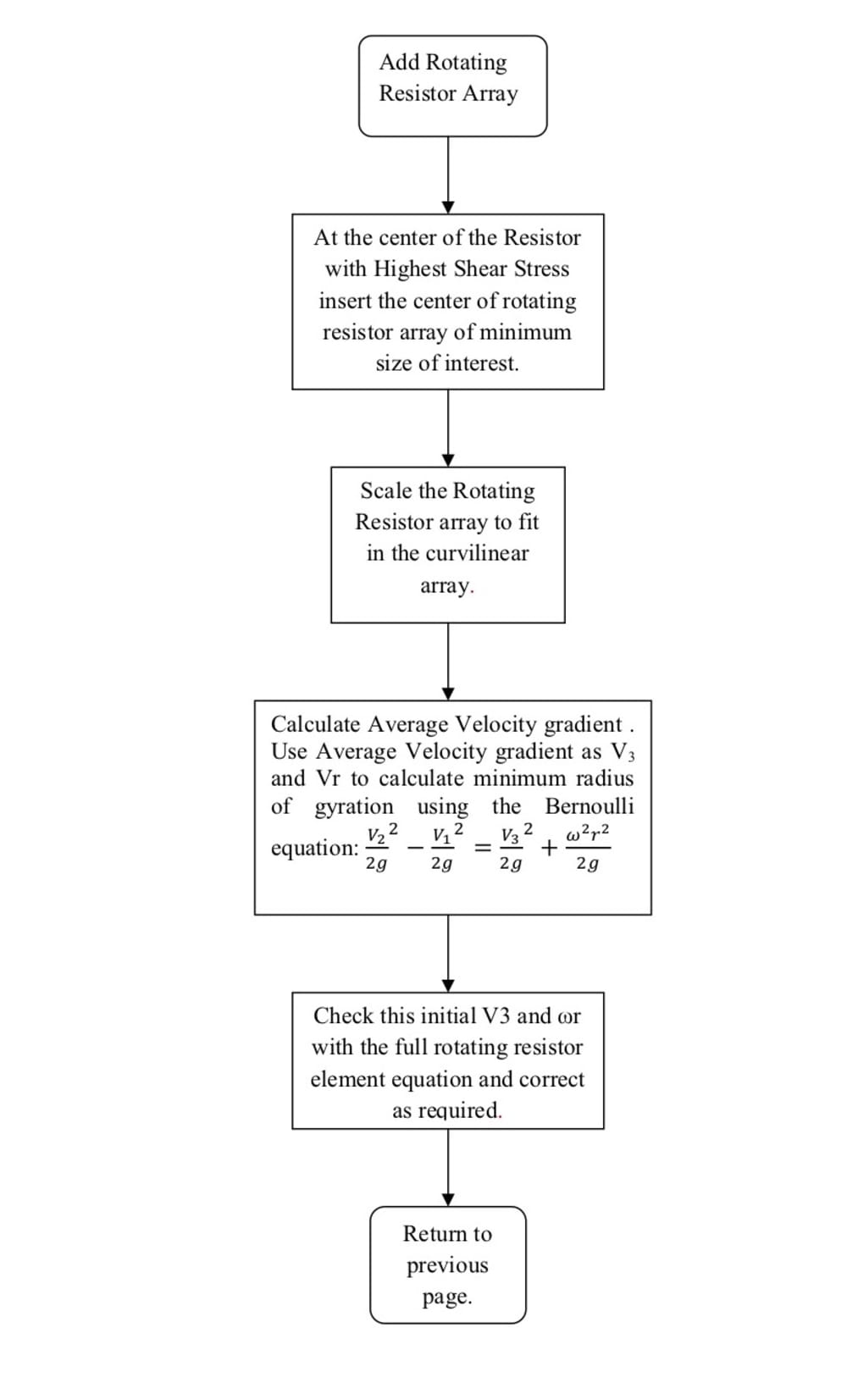
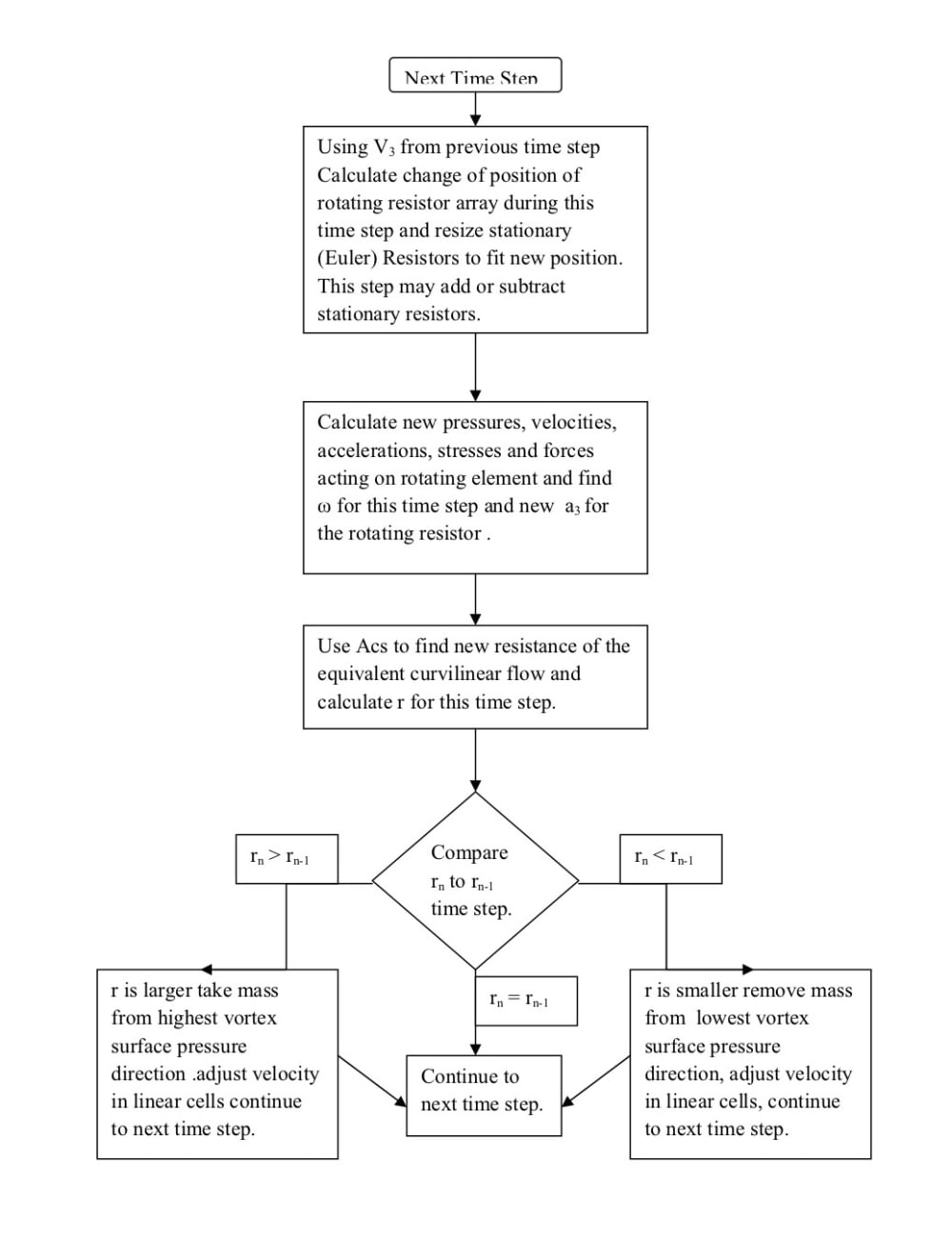
Forming an eddy where F is the force acting at the radius r and spinning at an angular rate ω. The attached illustration gives the process of how this calculation can be carried out.
Navier-Stokes is based on the fact that the total energy in a closed system is equal to a constant; so the time rate of change of energy of such a system is zero. Thus a closed system conserving power has a total power of zero.
Linearity allows elements to move through the computational domain over time. Particles, eddies and moving boundary are easily modeled. Forces due to electric and magnetic fields can easily be added allowing modeling of plasma.
Software based on conservation of power uses flow conditions to define element positions and number making use by non experts possible. Problems involving moving boundary conditions such as internal combustion engines, aero-elasticity, biologic flows, animal locomotion, can all be solved with the least computational burden.
Developing a software tool based on conservation of power has the potential to change life in ways we can not imagine.
Like this entry?
-
About the Entrant
- Name:John Snider
- Type of entry:individual
- Software used for this entry:It is a mathematical model used in software.
- Patent status:pending