Discovered Discrete Geometry Relationship between a Non-Regular Icosahedron and the other Five Regular Solids, of possible interest to Scientists.

Under the current exposure to the virus [corona] conditions one should not hesitate learning possibilities of accepting and use of new discoveries and particularly those bearing “change of paradigm,” with the involvement of discrete geometry.

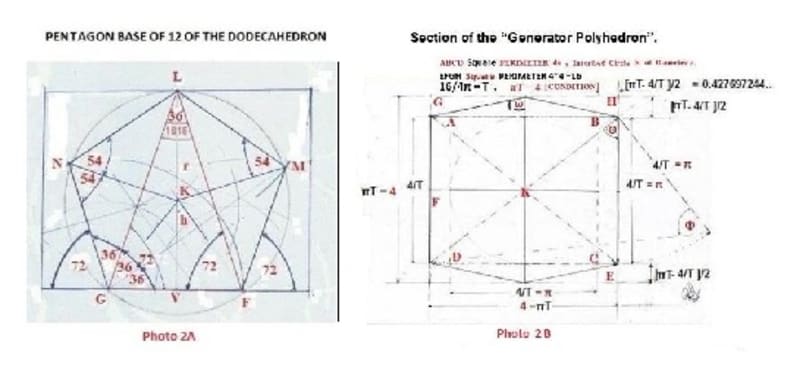
The Non-Regular Icosahedron, or otherwise the “Generator Polyhedron” [ PHOTO 1], a new Discovered Invention [2017] by Panagiotis Stefanides.

“Generator ” refers to the geometric characteristic of this Solid found to be the root upon which other Solid Polyhedra are based i.e. the Platonic/Eucleidean Solids [Icosahedron Dodecahedron etc.] The Geometry of this work is part of book: [ISBN 978 – 618 – 83169 – 0 - 4], National Library of Greece , 04/05/2017, by Panagiotis Ch. Stefanides.
From the geometry of the “Generator Polyhedron” [ Photo 1A, 1B, 2B, 3]
https://contest.techbriefs.com/2017/entries/aerospace-and-defense/8160
we find relationships:
3 parallelegrammes vertical to each-other. Sides’ lengths, of each parallelogramme, are in ratio of 4/π = 1.27201965 [for π = 3.14460551 i.e. 4/ SQRT(Golden Ratio)].
[4/2]/ [π/2] =[π/2]/ x, x = {[π/2]^2}/[4/2] = 2.472135953/2 = 1.23606797
Similarly the Icosahedron Parallelogramme ones are in ratio of 1.618033989 and those for the Dodecahedron are in ratio of 2.618033989.
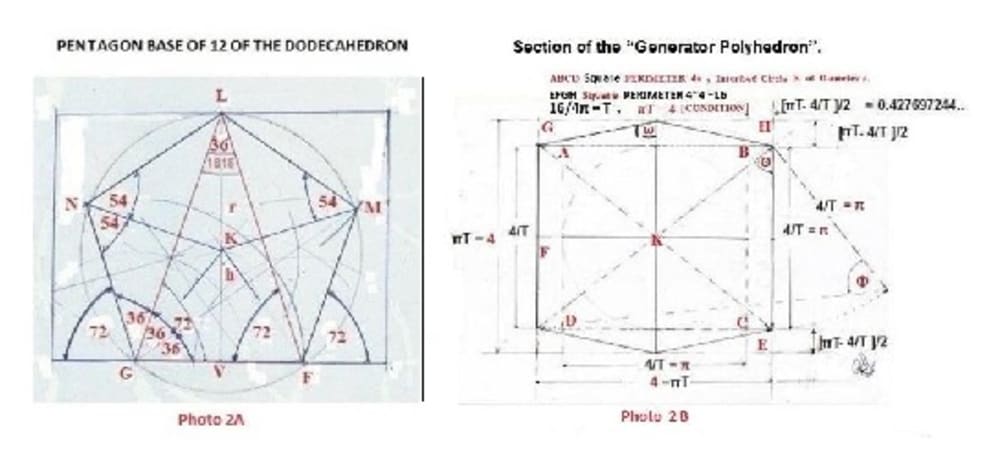
Relationship with the Dodecahedron Pentagon [Photo 2A].
Considering:
[4/2]/ [π/2] = [π/2]/ x, x = {[π/2]^2}/[4/2] = 2.472135953 / 2 = 1.23606797
{ [ π/2] / χ is the the dimenstional ratio of each of the 3 plains of the next smaller polyhedron skeleton structure – quantized reduction copy of the model}

1/8]*{4/[sqrt{ [sqrt(5) +1]/2}]}^2 = [ 1/sin(54)]

[1/8]*{4/[sqrt{ [sqrt(5) +1]/2}]}^2 = [3+sqrt(5)] / [ 2+ sqrt(5)]

1.236067977 = 1/ [Sin (54)] = x

This is directly Related to the Pentagon Angle of 54 Deg:
1/Sin(54) = 1.23606797

r = [½]/Cos(54) = 0.850650808, h = rSin(54) =0.68819096 , r/h =1/Sin(54) = x
H = r + h = 1.538841768, h/r = 1/x = Sin(54) = 0.809016994

r/h = { [ ½]/Cos(54)}/ rSin(54) = 0.850650808 / 0.68819096 = 1.23606797 = 1/Sin(54)

Photo 1: Generator Polyhedron and Skeleton Structures.
Photo 2: Pentagon of Dodecahedron and Section of the “Generator Polyhedron”.
Photo 3: “Generator Polyhedron” Stereometric Calculations.
You Tube Video Clip :
https://youtu.be/NuNuNySN2sU?t=9

Generator Polyhedron Skeleton Proposal[ by Panagiotis Stefanides] of Structure involving the 7 circles of Plato’s Planets [Plato’s Republic XIV 616 E -617A].