GEOMETRIC APPROACH TO GRAVITY FORCE VARIATION WITH HEIGHT By Panagiotis Stefanides

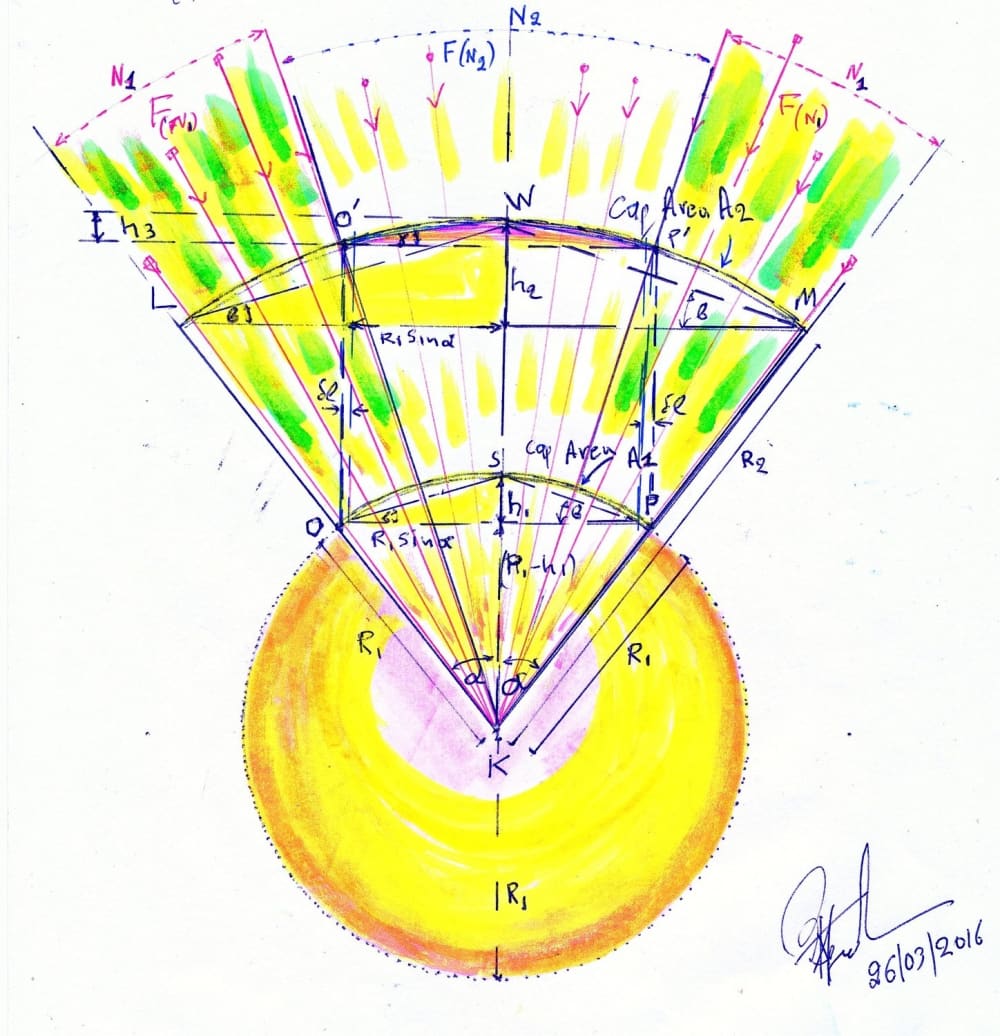
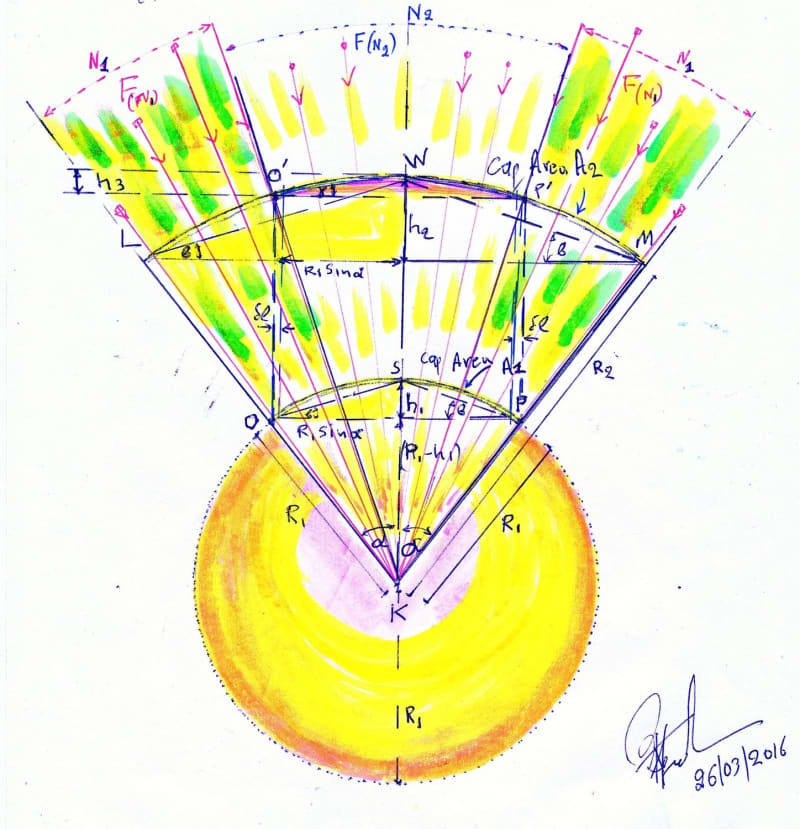
SPHERICAL SECTORS [Spherical Caps and Cones] R1 Earth’s Radius
Spherical Sectors [ LO΄WP΄M], [O΄WP΄] and [OSP].F(N) Gravitational Field Lines of Force passing via Caps.N Lines Emanate from K [ Earth’s Center f Gravity ].
N Lines pass, in total, via Cap OSP and Cap [LO΄WP΄M].
N2 Lines passing Cap [O΄WP΄].
N1 Lines miss passing via Cap [O΄WP΄].
A1 = Area of Cap OSP = 2π[R1][h1] = 2π[R1][(R1)(sin{α})(tan{ β})].
A2 = Area of Cap [LO΄WP΄M] = 2π[R2][h2] = 2π[R2][ (R2)(sin{α})(tan{ β})].
RATIO A2/A1 = [( R2)/ ( R1)]^2
Area A3, Cap [O΄WP΄], part of Cap [LO΄WP΄M], chosen Equal to that of Cap [OSP].

Note:
Cap [O΄WP΄] is a reflection of Cap [OSP] with same Area but with a Geometrical Configuration Complying with R2 Radius Curvature Compatible with Verticality of Lines of Force i.e. with h3h1 and Chord [O΄P΄]> [OP], { [O΄P΄]- [OP] = 2δl }.
Value of h3 may be found by:
specifying 2π[R2]h3=Area A1, and then finding from R2 Circle [O΄P΄]
[ circle power of a point theorem]:
{ [O΄P΄]/2}Squared = [h3][ 2R2 – h3].

Finally:
N Lines of Force pass via Area A2 and N2 Lines pass via Area A3 [=A1].
So N2 Lines = N[ A3/A2] = N[A1/A2],
thus, N2/N = [ A1/A2] = [( R1)/ ( R2)]^2 or
N/N2 =[ R2/R1]^2

Gravitational Lines [ N ] form the Vector Field describing the Gravitational Force [ F] applied to a unit Mass [ m ] at a point in space is its Gravitational Acceleration [ g ] at this point [ F/ m = g ].
Considering Areas of Caps as Masses of Unit Thickness [t= 1] and Unit Density[d=1 ],
Force on Cap [OSP ]/ [1.1.Area A1] =F(N)/[1.1.A1] = g(s) = g(e)
[g(e) = g(s) at point S on Earth’s Surface]
and
Force on Cap [O΄WP΄]/ [1.1. AreaA3] =F(N2)/[1.1.A3] =F(N2)/[1.1.A1] = g(w) and,
Ratio:
F(N)/[1.1.A1]} / {F(N2)[1.1.A1]} =F(N)/F(N2) = g(s)/ g(w)
g(s)/ g(w) =[(R2)/(R1)]^2
or
g(w) = g(s)[( R1)/ ( R2)]^2

Note:
Similarly for Cap [ LO΄WP΄M] and Cap [ OSP ]:
RATIO A2/A1 = [( R2)/ ( R1)]^2 =F(N)/F(N2) = g(s)/g(w) and,
F(N)/F(N2) =[ R2/R1]^2 = g(s)/g(w) , then
g(w) = g(s)[ [( R1)/ ( R2)]^2

© Copyright 2016, Eur Ing Panagiotis Chr. Stefanides CEng MIET