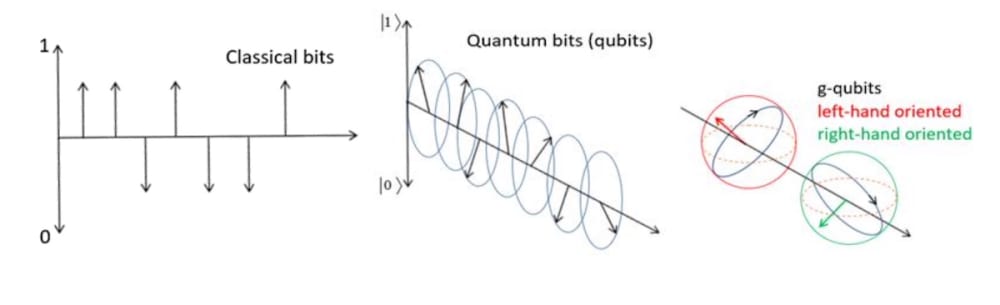
Quantum computers and quantum cryptography are potentially the first commercial applications of quantum physics. Unfortunately, quantum mechanics in its existing formulation is a no-work-around obstacle to bring these potential applications into reality. The theory needs to be reformulated in adequate logical and mathematical formalism. We see no successful, reliable results yet in creating quantum computers due to working with bad, inappropriate tools.
The instant of time when Clifford translation is applied to states makes no difference because resulting state is simultaneously redefined for all values of time, particularly also backward in time. That is obvious demonstration that the suggested theory allows indefinite event casual order. In that way the very notion of the concept of cause and effect disappears, thus we might not perceive time.
Further, we get superiority of the suggested theory over classical computations because all measured observable values get available all together, not through looking one by one. Simultaneous availability has always been the proof of calculational supremacy of hypothetical qubit entangled quantum computers. The current approach transcends those computational schemes also since the latter have tough problems of creating large sets of qubits. In the current scheme any number of test observables can be placed into continuum of the time/space dependent values of the spreon state, thus fetching out any number of values spread over three-dimensions and at all instants of time not generally following cause/effect ordering.
Thus, quantum computer built in the current theory approach is a kind of analogue computer, aimed, first of all, at modeling three-dimensional vector fields.
Two seminal ideas – variable and explicitly defined complex plane in three dimensions, and the states as operators acting on observables – allow to put forth comprehensive and much more detailed formalism appropriate for quantum mechanics in general and particularly for quantum computing schemes.
Special solution of the Maxwell equation(s)in the geometric algebra frame particularly gives state, spreon, spreading over the whole three-dimensional space for all values of time, along with the results of measurement of any observable.
Like this entry?
-
About the Entrant
- Name:Alexander Soiguine
- Type of entry:individual
- Patent status:none