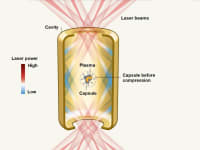
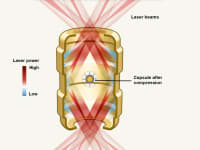
In nuclear fusion, two nuclei of light atoms, generally hydrogen and its isotopes (deuterium and tritium), join together to form another heavier nucleus. These reactions can release pollution-free fusion energy. An example of fusion reactions are those that take place in the sun, and its necessary to reach high energy levels that allow the nuclei to approach very short distances in which the force of nuclear attraction exceeds the forces of electrostatic repulsion. To do this, the following requirements must be met: 1) Its necessary to heating the atoms until achieving a plasma, composed of free electrons and highly ionized atoms; 2) To guarantee the confinement and control of the plasma at high temperatures in the cavity of a fusion reactor for the time necessary for the reaction to occur; and 3) Its also necessary to achieve sufficient plasma density so that the nuclei are close to each other and can give rise to fusion reactions.
Inertial confinement fission (ICF) consists of creating a medium so dense that the particles have almost no chance of escaping without colliding with each other. To do this, a small sphere composed of deuterium and tritium is impacted by a laser beam, causing it to implode. Thus, it becomes hundreds of times denser than in its normal solid state, allowing the fusion reaction to occur.
Researchers at the National Ignition Facility at Lawrence Livermore National Laboratory in California were able to spark a fusion reaction that was sustained briefly with 192 lasers and temperatures more than three times higher than the center of the sun, a milestone.
My idea is to use chaos theory, and fractal models to solve the steps of increasing difficulty such as burning plasma, ignition, and energy gain. The study of turbulence in flows like flames and plasma is adapted to fractals; and we could stabilize the plasma flow created by the lasers when the fuel capsule is heated. Turbulent flows are chaotic and very difficult to model correctly, so a fractal representation of them could helps engineers and physicists to better understand these flows.
Control of Chaos: This is the stabilization, by means of small system perturbations, of one of these unstable periodic orbits. The result is to render an otherwise chaotic motion more stable and predictable. Two basic techniques approaches developed require a previous determination of the unstable periodic orbits of the chaotic system before the controlling algorithm can be designed.
OGY Method: Here, the infinite number of unstable periodic orbits typically embedded in a chaotic attractor could control by means of applying only very small perturbations. In this method, small, wisely chosen, kicks are applied to the system once per cycle, to maintain it near the desired stable periodic orbit.
Pyragas Method: In this method of stabilizing a periodic orbit, an appropriate continuous controlling signal is injected into the system, whose intensity is practically zero as the system evolves close to the desired periodic orbit but increases when it drifts away from the desired orbit.
Like this entry?
-
About the Entrant
- Name:Guillermo Perez
- Type of entry:individual
- Patent status:none