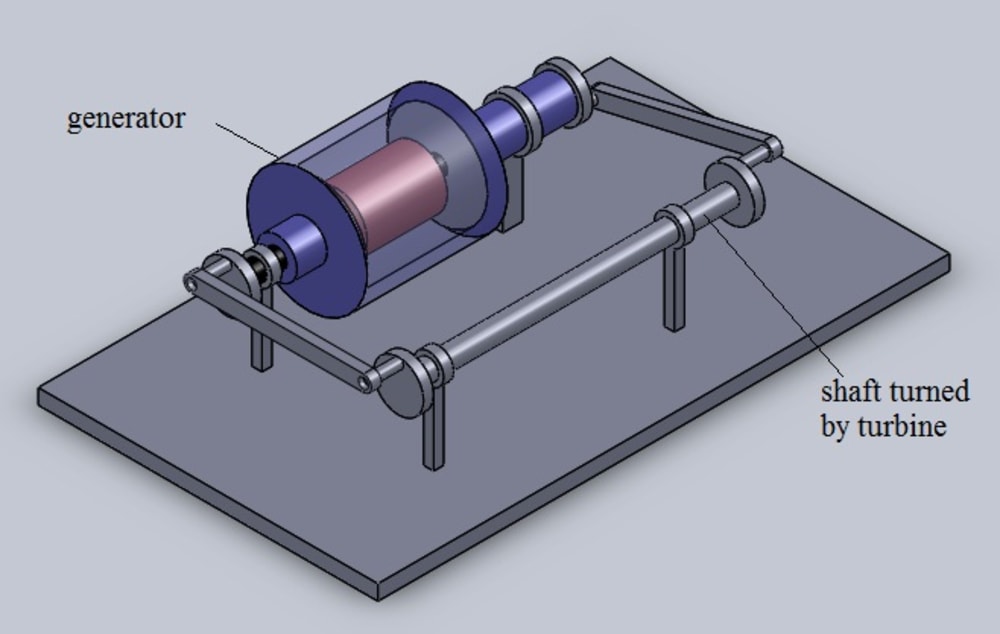
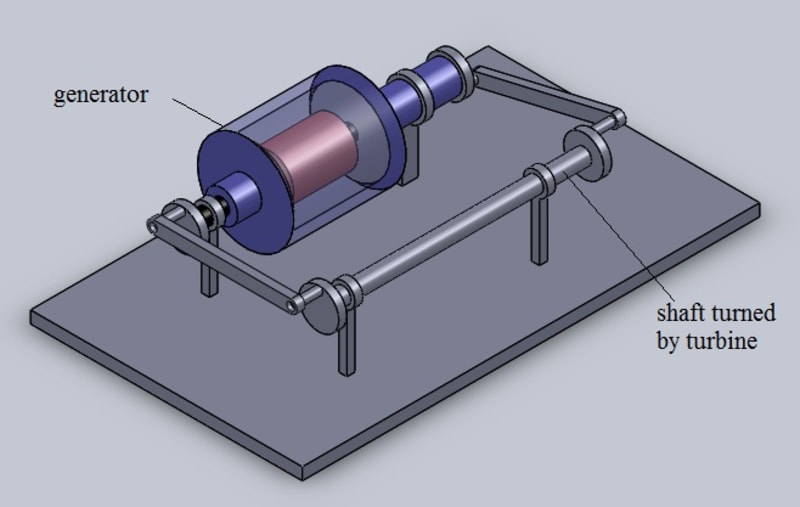
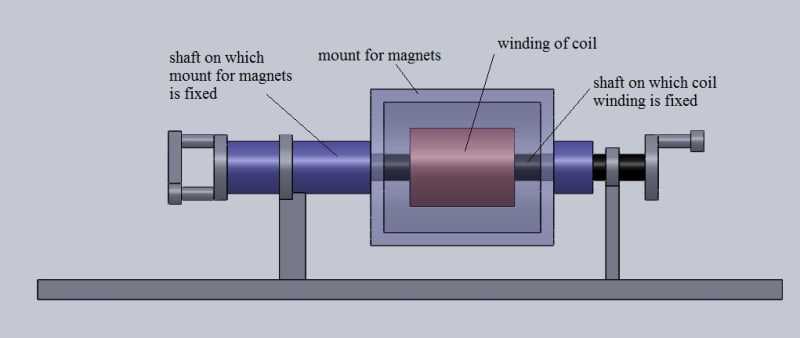
The generators that we have today consist of an armature that rotates and a stationary object. Either the magnetic field is rotated and the coil is kept stationary or vice-versa.
The basic principle of a generator is to produce change in magnetic flux linked with the coil. The more the change, the more voltage produced.
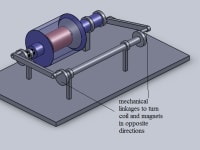
In this model, both the magnet housing and the coil are rotated but in opposite directions.
In this way, the relative velocity between the magnets and the coil is doubled.
Since the relative velocity between the magnets and the coil is doubled, the magnetic flux change will also double.
Now, if the magnetic flux change is doubled, then the e.m.f. induced will also be doubled.
If the e.m.f. induced is doubled, then the power generated will twice.
Now, to turn both the coil and the magnet housing, an increased torque is required.
But the energy required to increase the torque is way less than the increase in energy obtained.
Calculations for the above fact are shown next.
e = - N (d?/dt)
Where,
e – e.m.f. induced
? – flux
t – time
N – number of turns
Now flux change is doubled, so e will also be doubled.
P = V I
Where,
P – power generated
V – potential difference across load
I – Current
As you can see when V becomes 2V then, power becomes 2P.
A CAD model of the generator was drawn and the mass of the coil and the magnet housing was calculated.
Mass of magnet housing : 50 kg
Mass of coil winding : 30 kg
Equating energy of the turning body and the energy required to turn the shaft:
0.5 * I * w2 = T * w
Therefore,
T = 0.5 * I * w
Where,
I – moment of inertia
w – angular velocity
T – torque
Now, radius of magnet housing = 27.5 cm
Radius of wire winding = 20 cm
Torque required to turn magnet housing :
T = 0.25 * 30 * (0.275)2 * w
T= 1.46 * w
Where w is the rpm at which the magnet housing should be turned
Torque required to turn coil winding:
T = 0.5 * 50 * (0.20)2 * w
T= 1 * w
Therefore, the total torque required is
T =2.46 *w
Where, w is the rpm
This is the excitation torque required. After the speed has been obtained, the torque required will reduce.
Thus, with this innovation, we can obtain a generator which will give you the power that is equivalent to running the conventional single rotor generator at twice the speed.
Like this entry?
-
About the Entrant
- Name:Vibin Varghese
- Type of entry:individual
- Software used for this entry:Solid Works
- Patent status:none