The need to interest would-be students in the apparently complex subject of macroeconomics is considerably eased, when they can see and play with a mechanical model that represents the whole of our social system. This model, being presented here, comprises of a compound balancing machine, which achieves this aim by representing our social system in terms of its various economic exchanges.
The millions of activities being performed by citizens of a country over a period of time, are actually of only 19 different kinds (see the recent book: "Consequential Macroeconomics--Explaining About How our Social System Works", by David Harold Chester). Taking average levels of these idealized activities, only 6 kinds of role-playing entities are needed to provide the need for them. The 6 entities are:
Landlords, Householders, Producers, Capitalists, Banks and Government.
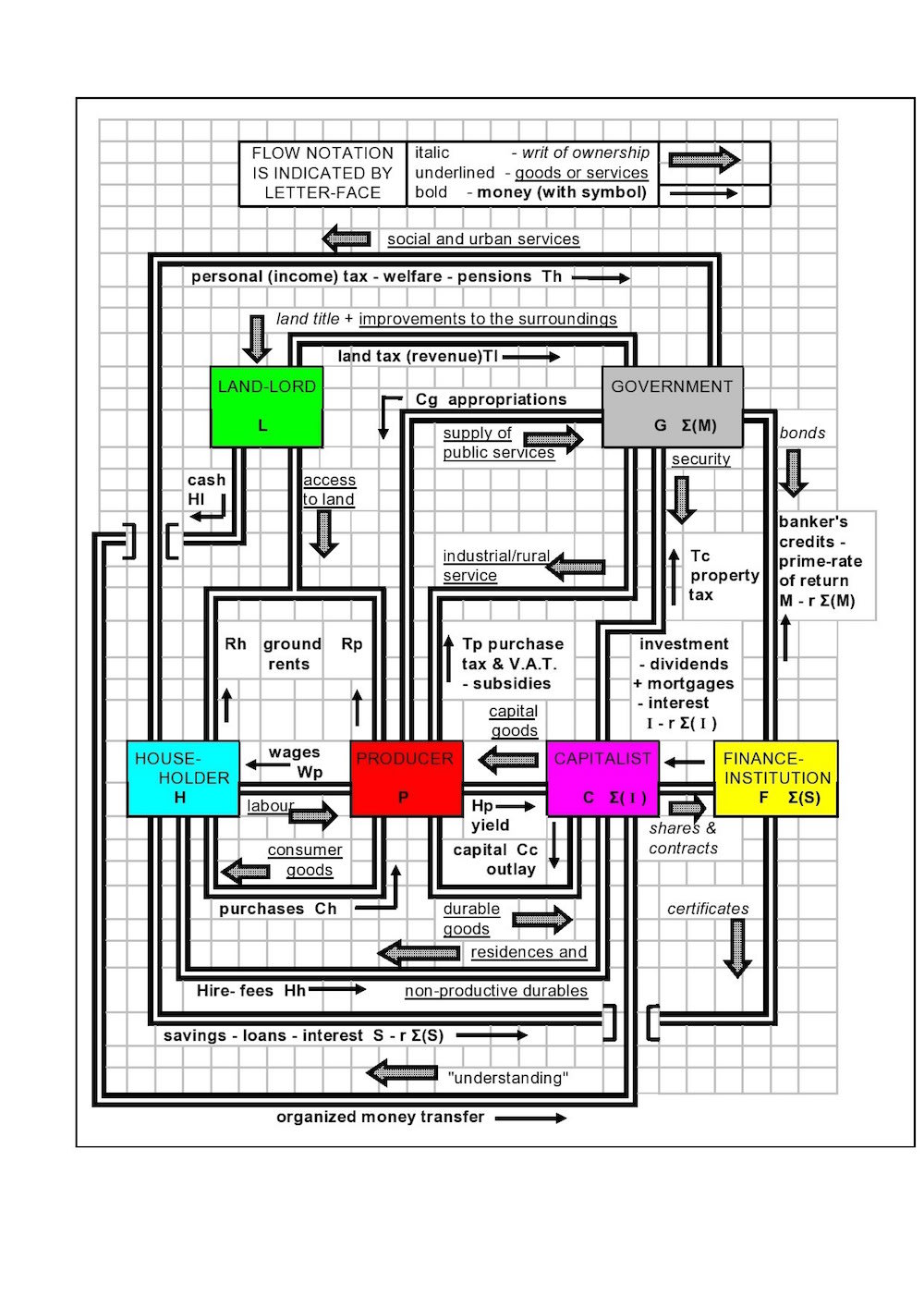
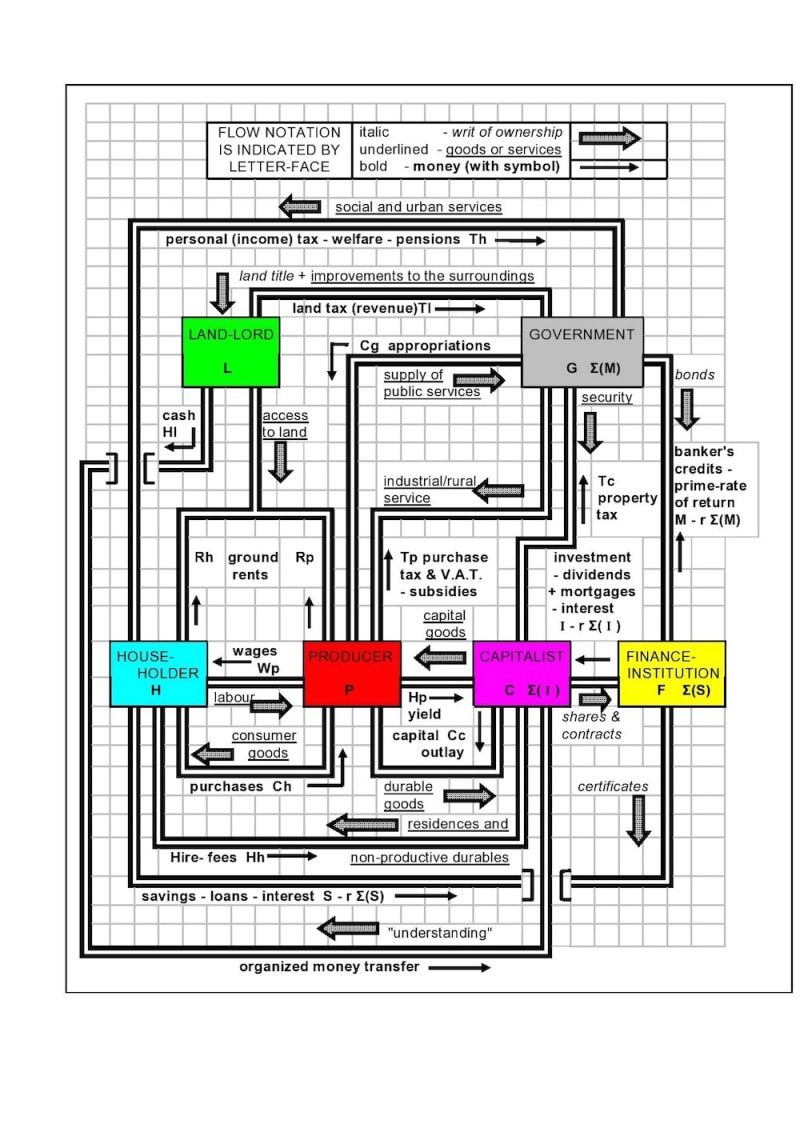
These individual kinds of entities have incoming and out-going money flows, and from Nobel Laureate W.W. Leontief's input/output money-flow theory, each entity balances its rate of money passage (see "The Choice of Technology", Scientific American, Vol.252, no.6, June, 1985). The money is always spent, loaned, invested, etc., rather than it being hoarded, which has no economic advantage. A diagram illustrating this situation is presented in Figure 1.
In the mechanical model, each entity is represented by a balancing-beam having arms of equal length. The ends of each beam are pulled down through cords, due to the gravitational forces acting on weights (for which different numbers of similar coins can be used), which are placed in specific carriers. Each weight represents the amount of money being exchanged, over a the same time-interval, for one of the 19 kinds of our economics' activities, such as earnings, taxes, purchases, investments, etc. The weights and carriers are suspended by pulley-wheels on cords, see figures 2 and 3. All the input money is arranged to pull on one end of a particular beam and the output money pulls on the opposite end. The beams are balanced when the macroeconomics system is in a state of equilibrium.
To achieve this (happy) condition additional weights need to be added or removed from the carriers, but each change affects two beams and on balancing one it tends to unbalance another! The mathematical problem presented to the students is to work out what combination of all 19 weights will allow the economy to be in a steady state and possibly what a government can do in order to manage this, when there is an imbalance of its money-flows--that is when there is a surplus or a deficit in the budget (or, for that matter, in the balance-sheets of any of the other entities).
Like this entry?
-
About the Entrant
- Name:David Harold Chester
- Type of entry:individual
- Software used for this entry:none
- Patent status:none